Frequently Asked Questions

What types of computational values are used by the VFC DLOM Calculator® for estimating marketing periods and price volatility?

The values are means and standard determined for selected marketing period parameters.

What is the source of the computational values provided by the VFC DLOM Calculator® for estimating marketing periods?

The computational values provided by the VFC DLOM Calculator® are derived from the BIZCOMPS® transaction database.

Are the BIZCOMPS® computational values provided by the VFC DLOM Calculator® up to date?

Users can ensure that marketing period parameters used in the VFC DLOM Calculator® are up to date by making their own calculations of marketing period parameter values upon subscribing to the BIZCOMPS® transaction database.

Can means and standard deviations derived from other sources be used in the VFC DLOM Calculator®?

Yes, the VFC DLOM Calculator® can be used with marketing period parameters and computational values derived from any source. Simply enter the estimated mean and standard deviation in the appropriate input field for the VFC estimator or calculator you are using.

What alternative sources of marketing period computational values are available besides BIZCOMPS®?

Comparable values can be derived from the Pratt’s Stats® transaction database upon subscribing to the Pratt’s Stats® service, and perhaps other public and private sources.

How do I input alternative marketing period computational values in the VFC DLOM Calculator®?

An input screen is provided for each estimator and calculator.

Marketing Period Estimator

Price Volatility Estimator

Single Probability DLOM Calculator

Double Probability Estimator

Double Probability DLOM Calculator

What applications of the VFC DLOM Calculator® will accept alternative marketing period and price volatility computational values?

All of our marketing period and price volatility applications will accept alternative values. Simply enter the means and standard deviations you want to use in the applicable input boxes.

Marketing Period Estimator

Price Volatility Estimator

Single Probability DLOM Calculator

Double Probability Estimator

Double Probability DLOM Calculator

What is the source of the computational values provided by the VFC DLOM Calculator® for estimating price volatility?

The computational values provided by the VFC DLOM Calculator® are derived from the split adjusted closing prices of publicly traded guideline companies selected by users.

Can I provide my own estimates of price volatility?

Yes, an input field is provided for that purpose.

Can I select a time period from which the VFC DLOM Calculator® will determine price volatility parameters?

Yes, input fields are provided to enter a range of dates.

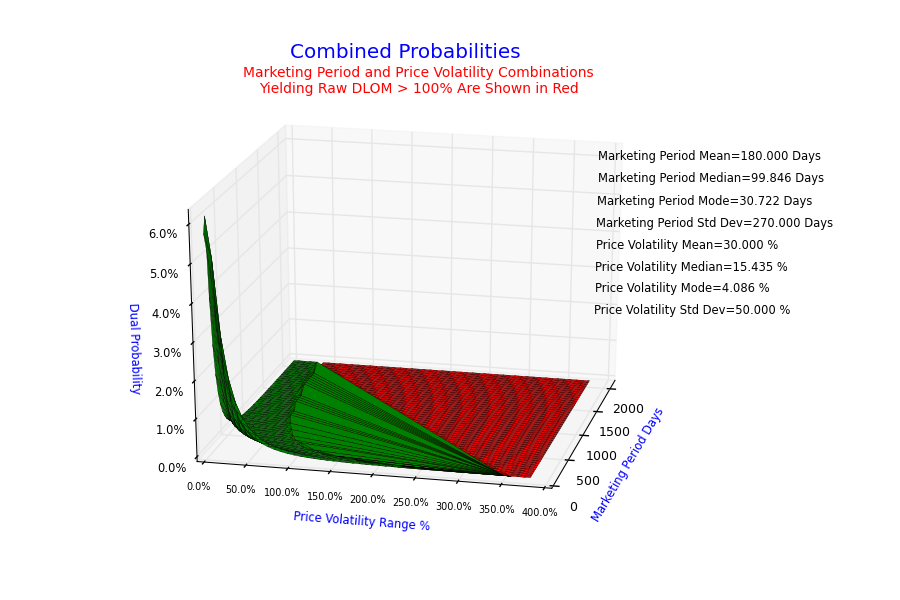
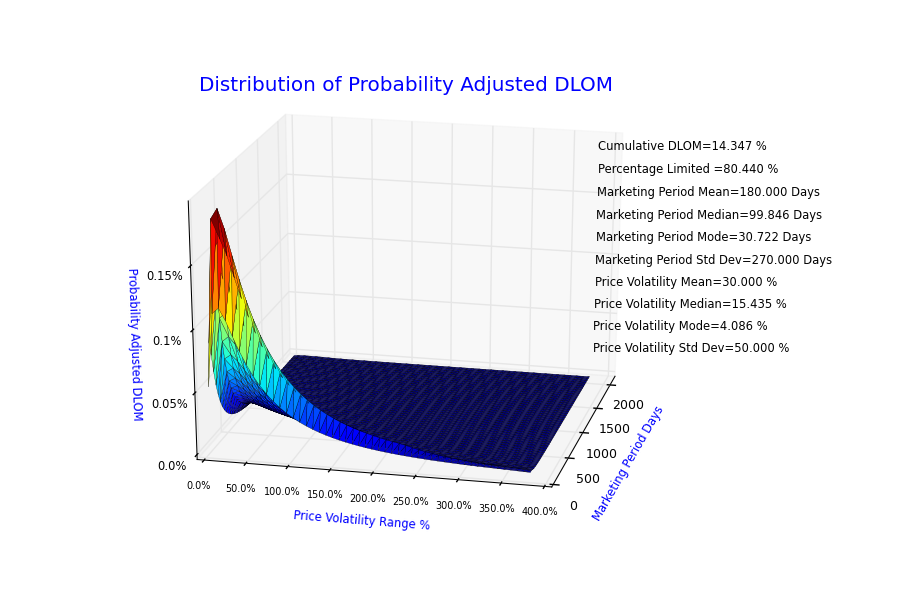
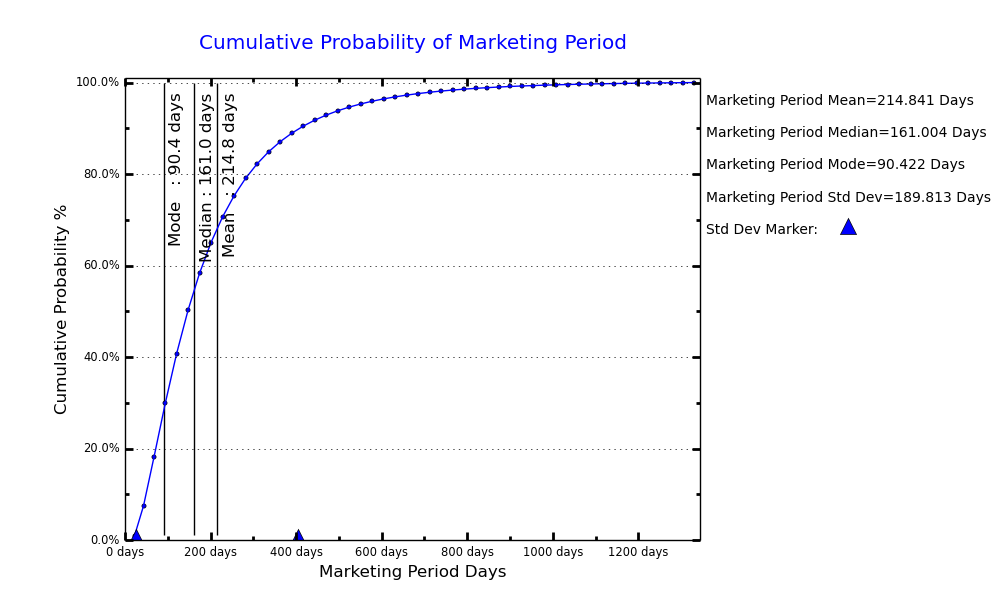
Does the VFC DLOM Calculator® report the values from which the various graphs are made?

Yes.

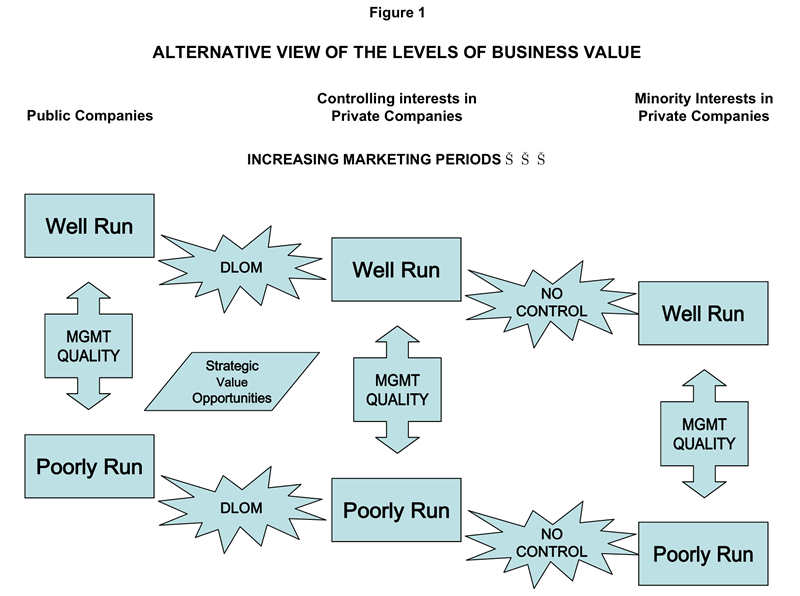
Should DLOM be applied to controlling interests of privately held businesses?

Yes. The graph below shows how well run and poorly run private companies relate to each other and how the opportunity to realize strategic and synergistic values arises from the conversion of poorly run firms into well run firms. The graph demonstrates that all privately held companies – even controlling interests – are subject to DLOM. Assuming two otherwise identical firms, the minority interest is subject to a larger DLOM that the controlling interest if it would take longer to sell the minority interest.

Why is there no Listing Year selection in the VFC DLOM Calculator® input pages?

Our experience is that BIZCOMPS® data (and Pratt’s Stats® data) lag current years as transactional information is acquired and added to the database. You may be able to obtain sufficient recent year data by subscribing directly to BIZCOMPS®. You can then input the parameter values that you determine directly into the VFC DLOM Calculator.™

Can I mix parameter values that I provide with parameter values provided by the VFC DLOM Calculator®?

Yes, but only one set of values is allowed per parameter.

Option models measure liquidity over time. Should an increment be added to DLOM to reflect the basic economic hurdle of an Initial Public Offering?

If a business can be sold at any price then the basic concept of marketability is met.  Therefore, the lack of liquidity associated with the marketing period is precisely the correct measure of DLOM.  The appropriate questions are: (1) How long will it take to sell the business?, and (2) What price risk is associated with the marketing period?  Properly crafted DLOM analysis seeks to address and answer those questions.

VFC views the DLOMs calculated with the VFC DLOM Calculator® as systematic.  Therefore, depending on the circumstance, it would not be inappropriate to add an increment to cover non-systematic circumstances.  But adding an increment to DLOM for what appears to be the cost of going public is an area that is fraught with valuation risk, and is highly debatable.  Should the costs of a private sale be used instead?  Or in addition?  VFC’s position is that none of the above is appropriate.  It is generally accepted that Fair Market Value (FMV) is the price at which the asset changes hands.  That is the contract price concept.  Think about selling a house.  FMV = sales price = contract price = price before commissions and closing costs.  Deducting such costs ignores the fact that the buyer is paying a price that is before such cost.  So if you include such transactions costs as a deduction then you appear to have deviated from FMV by determining the price realized by the seller instead of the price agreed-upon by the buyer and the seller.

It is VFC’s position that the appropriate reconciling item between publicly-traded and private securities is not the “basic economic hurdle of an Initial Public Offering” or the basic economic hurdle of a private sales.  Instead, the reconciling items are (1) the time difference necessary for a successful marketing a private security versus a comparable publicly-traded security at the “as if marketable price,” and (2) the non-systematic differences between the private company subject and the public companies that are the guidelines for price volatility.  Professionals should consider:

• Are there non-systematic reasons that the appraisal subject will take a longer (or a shorter) time to sell than the benchmarks provided by BIZCOMPS, Pratt’s Stats, or by a public offering alternative?

• Are there non-systematic differences, such as debt-to-equity or profitability ratios, that would increase (or decrease) price volatility relative to the guideline public companies or indexes?

Those are the appropriate points of adjustment to arrive at a well crafted DLOM conclusion.  Those questions can be analyzed objectively, and, once answered, the appraiser can apply “reconciled” inputs to the option formulas available in the VFC DLOM Calculator®.  This approach allows appraisers to avoid adding the uncertainty of just adding some arbitrary factor to DLOM. 

Start my FREE TRIAL