fbpx

Empirical Research

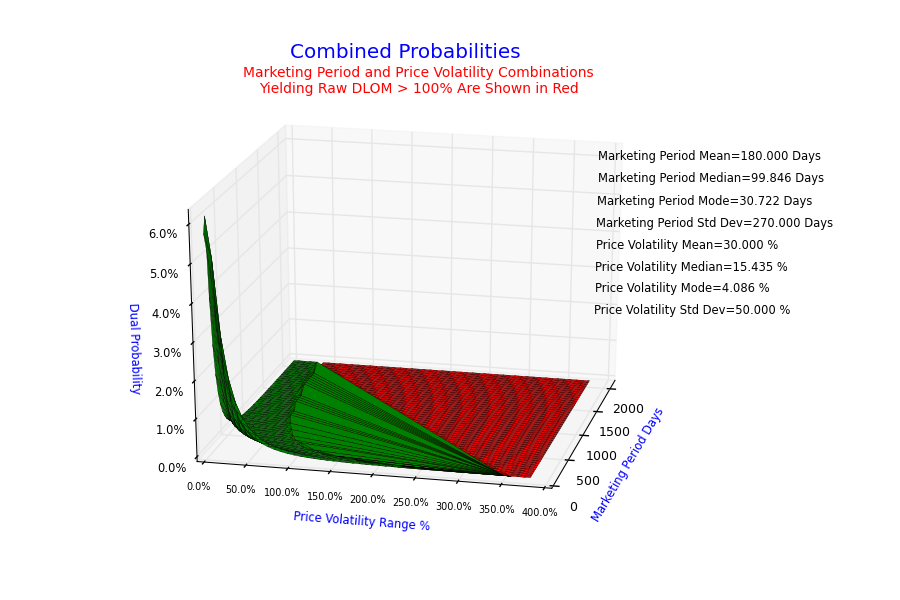
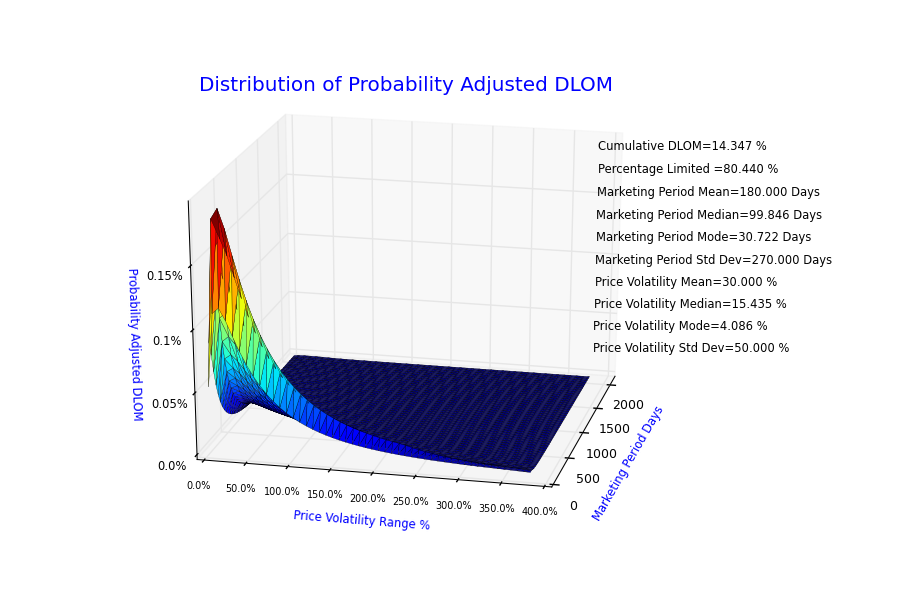
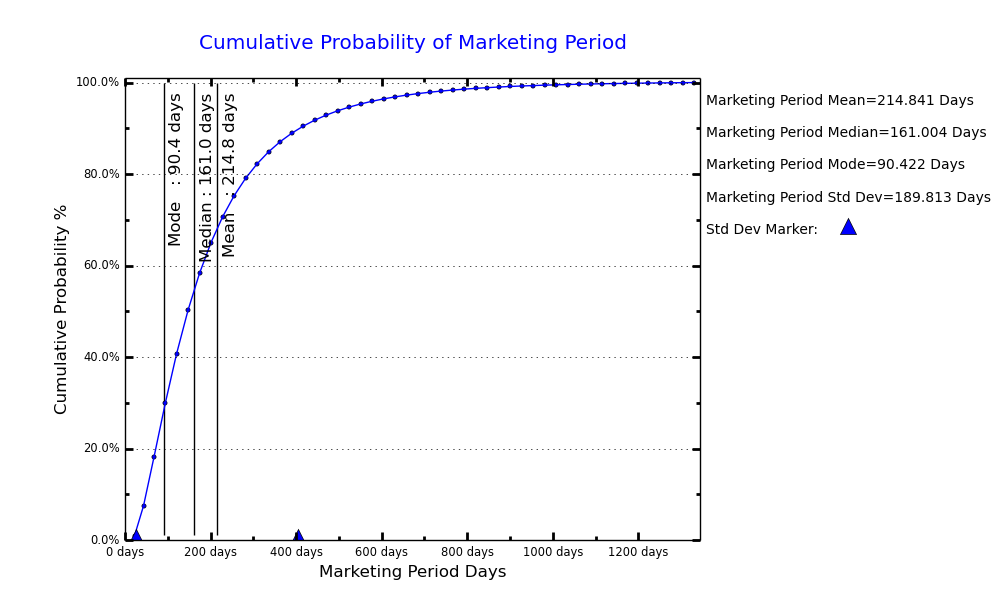
VFC’s proprietary DLOM calculator combines probability-based time and price volatility variables in conjunction with the Longstaff, Black-Scholes, and Finnerty option formulas to yield highly refined, objectively determined DLOM estimates that are valuation-date specific.

Introduction by Francis A. Longstaff, Ph.D.

The question of how to value illiquid investments that cannot be traded continuously is one of the most challenging issues facing academic researchers and industry practitioners. The reason for this is that the lack of marketability takes us well outside standard paradigms in financial economics such as the notion of efficient markets, portfolio choice, and the usual risk and return tradeoffs that underlie much of modern investment theory.

Marc Vianello’s book “Empirical Research Regarding Discounts for Lack of Marketability” is an impressive effort to bring a rigorous and comprehensive data-based perspective to addressing these issues. The book begins with a thorough review of the historical research on the topic and provides valuable insights about the scope and reliability of the evidence. The book then moves on to an insightful analysis of the strengths and weaknesses of existing models of the discount for lack of marketability. What makes this analysis particularly valuable is the depth of knowledge and practical experience the author brings to the task. Finally, the book offers a number of carefully considered extensions to existing models, demonstrates how these can be implemented in practice, and evaluates their performance using objective empirical standards.

This book makes great strides in helping us understand the nature of the discount for lack of marketability phenomenon and offers us valuable perspectives on how to address the associated challenges of valuation.

Francis A. Longstaff, Ph.D.
Allstate Chair in Insurance and Finance
Anderson School of Management
University of California at Los Angeles


Introduction by Michael Gregory, ASA, CVA, MBA

With a dedication to improve analytics for business valuers, Marc Vianello has diligently and passionately conducted his research on Discount for Lack of Marketability over many years. As a result of his research he has shed light on the shortcomings of many existing models, and he has developed a tool that is based on real world data and that has been accepted by the courts.

After a careful look at the literature followed by a critique of major sources commonly used by business valuers, the author presents very significant findings. An analysis of the data with graphs, charts and statistical measures presents reasons to question currently accepted approaches. Starting with Longstaff model probability is incorporated into a new model considering the mean and standard deviation of market timing and volatility. The author presents how to obtain these measures from existing data sources (systemic) and provides the business valuer with insights with how to consider the application of non-systemic professional judgment.

From the text the author states, “Double probability DLOMs calculated using the Longstaff formula provided values most consistent with the empirical evidence provided by the discounts of corresponding restricted stock transactions. The calculated DLOMs should be considered systematic. The currently available empirical information supports the conclusion that double probability DLOMs calculated using the VFC Longstaff methodology results in reliable estimates of systematic DLOM.” This is very significant in that no other source can make such a claim.

This is a tool that no business valuer should be without.

Michael Gregory, ASA, CVA, MBA
Former IRS Engineering Territory Manager
Champion of the IRS DLOM Job Aid